This is a quite technically-oriented article in which I will present an idea for possible superluminal communication, suitable for exercising the skills of critical thinking and objective analysis.
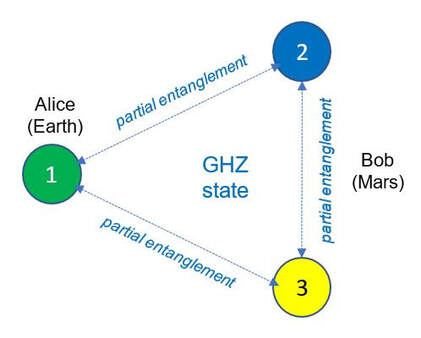
In order to circumvent the natural speed of light limitation, this approach exploits the so-called Greenberger–Horne–Zeilinger (GHZ) state of quantum entanglement. Unlike many previous attempts to use pairs of quantum-entangled particles for this purpose, this approach utilizes quantum entanglement of groups of three particles. There are two such states: the GHZ and W-state. I have to emphasize that this idea is not based on getting results of measurements of entangled particles in various settings or trying to somehow force the particle on one side into the desired quantum state (which is, of course, impossible). Instead, this approach is oriented toward discerning different amounts of entanglement in the tripartite GHZ (or even W-state) groups. If there is a system of three particles in the GHZ state of quantum entanglement, this essentially means that their quantum states are mutually correlated. However, the correlation between any of these two particles within the system is partial, while the entanglement of the system as a whole is full and stable. This reasoning has an important premise: whenever one of the particles within a GHZ system is measured along an orthogonal direction, it becomes disentangled from the other two. On the other “side” of the system, those two other particles become fully entangled with each other, i.e., they are left in a maximally entangled Bell state. On the other hand, whenever one of the particles within a GHZ system is measured along the privileged Z direction, the entanglement of all three particles is completely destroyed. This means that not only the measured particle is disentangled, but also the other two become unentangled from each other and from the first particle. In other words, they are left in a “pure” or “mixed” state.[1] In accordance with the basics elements mentioned above, this approach to FTL communication is presented below in the form of thought experiment. So, we may imagine that one of these particles is on Earth with Alice, who has suitable equipment for measurement. The other two particles of that system are with Bob, who brought them with him to Mars, also with appropriate measuring equipment. Although physically separated, all three particles have preserved their GHZ state of entanglement. [1] “Although a naive measurement of the third particle of the GHZ state results in an unentangled pair, a more clever measurement, along an orthogonal direction, can leave behind a maximally entangled Bell state. (…) The lesson to be drawn from this is that pairwise entanglement in the GHZ is more subtle than it naively appears: measurements along the privileged Z-direction destroy pairwise entanglement, but other measurements (along different axes) do not.” Source: Wikipedia, https://en.wikipedia.org/wiki/Greenberger%E2%80%93Horne%E2%80%93Zeilinger_state
In previously agreed time intervals, depending on the message that she wants to send to Bob, Alice takes a measurement on her one-particle part of the GHZ system. She measures its quantum state either along the privileged Z direction or along an orthogonal direction.
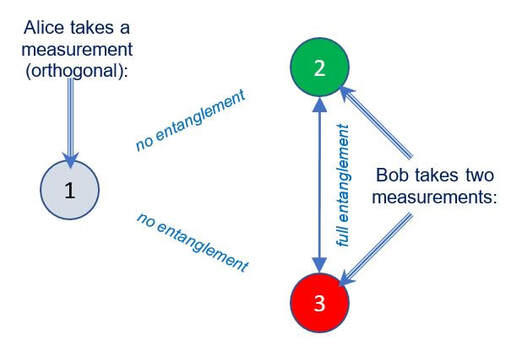
On Mars, Bob regularly takes separate measurements on his two particles in the same time intervals (previously agreed with Alice). If Alice takes the measurement along the orthogonal direction, her particle becomes unentangled from the other two on Mars, but Bob’s pair of two particles becomes mutually fully entangled. He measures both his particles separately, compares the results and learns that their quantum states are 100% in correlation. (Perhaps there should be several more such measurements on similar GHZ systems to determine whether the pairs are fully correlated or not.) Therefore, although no information is really being transferred from Earth to Mars, Bob instantly assumes that Alice has taken the measurement along the orthogonal direction because his particles are fully correlated, and this fact he translates into a simple message “YES” or, say, 1.
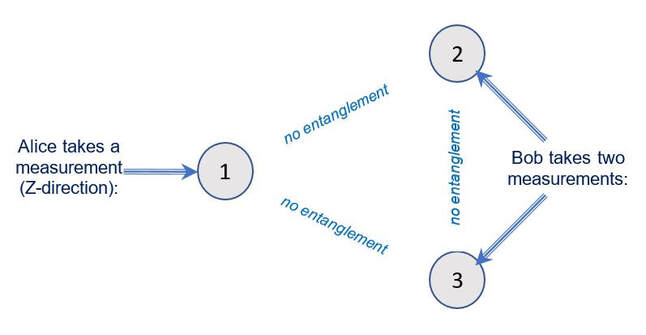
If Alice takes the measurement along the Z direction, Bob becomes aware of that because when he measures his pair of particles in the GHZ state and gets information on their quantum properties, he sees that they are disentangled from each other. As he now knows that Alice took the measurement along the Z direction, he translates this state of disentanglement between his two particles as “NO” or 0.
Alice and Bob may have arrays of these three-particle GHZ systems, each with one particle on Earth, and two particles on Mars, and vice versa. They use these arrays for multiple exchanges of simple information, and, if needed, for determining with high certainty whether two other particles in each system are fully entangled or not. Moreover, there should be multiple measurements for each side to ensure that the jitter of the measurement tools cannot reverse the order of measurements.
Note that a similar approach could be applied to another type of tripartite entangled state—the so-called W-state. In it, three particles are also entangled as a system, particles are mutually entangled to some extent, but when one takes a measurement on one of its constituents, that does not destroy the entanglement of the other two particles—on the contrary, the entanglement persists and even becomes full. In this case, also in regular, previously agreed time intervals, Alice either takes or skips her measurement. On Mars, Bob would always be taking measurements on his array of particles. If Alice had taken her measurement, he would have learned that his pairs of particles are fully entangled. He instantly knows that Alice had taken the measurement and therefore he assumes that the message is YES or 1. Conversely, if Bob’s results show that his pairs of particles are still partially entangled, it would mean that Alice skipped her measurement, thus he concludes that her message is NO or 0. It seems that, effectively, complex messages can be instantaneously exchanged between Alice and Bob in either of these ways. They would not have to wait fifteen or twenty minutes to get the information from the other planet. In a nutshell (for the usage of GHZ state of quantum entanglement): 1. There are three particles in the GHZ entangled state; 2. One of these particles is with Alice on Earth, the other two are with Bob on Mars; 3. Either:
In a nutshell (for the usage of W-state of quantum entanglement): 1. There are three particles in the W-state; 2. One of these particles is with Alice on Earth, the other two are with Bob on Mars; 3. Either:
DISCLAIMER: The laws of physics strictly forbid superluminal communication. This is only a mental exercise with the purpose of developing the skills of critical thinking and objective analysis. I invite readers, especially those with solid knowledge in the field of quantum physics, to closely scrutinize this thought experiment and let me know of any flaws in this reasoning in the comments section. Have a nice day! :-)
1 Comment
TGB
4/9/2020 23:40:54
We know the rules inside our universe: nothing goes faster than c.
Reply
Leave a Reply. |
Please note that most of the articles have a "Read More" break, which is sometimes hardly visible.
It is located at the bottom of visible part of the article, on the right side. To continue reading the article, click on that link. This page may contain affiliate links meaning we earn a commission if you use those links.
We only recommend pages we appreciate and trust. Archives
March 2023
Categories
All

|
For guest posts or placing ads on our website, please use the contact form on the 'About/Contact Us' page.


 RSS Feed
RSS Feed

